1.

비판정법을 이용하면, 수렴구간을 쉽게 구해줄 수 있다.
2.

멱급수 해법에서, 오일러-코시 모듈을 적용해줄 수 있는 형태이다.
정리하면 홀수 차항의 미정계수는 전부 0으로 사라진다.(1차항 제외)
그리고 짝수차항의 계수는 점화식 관계를 통해, a_0로 정리해줄 수 있다.
3.

푸리에급수 관련 파트이다.
오일러코시 미방을 상수계수로 바꾸어 고유함수를 구한다.
그 후 역치환을 통해 고유함수를 다시 구해준다.
4.

sin 함수간의 직교성을 증명하는 문제이다. 두 함수의 곱을 특정구간에서 적분하면 쉽게 직교성을 증명할 수 있다.
이때 정규직교집합에 속하는 함수들은 모두 크기가 1이라는 것을 이용하여, 정규직교 집합을 구할 수 있다.
5.
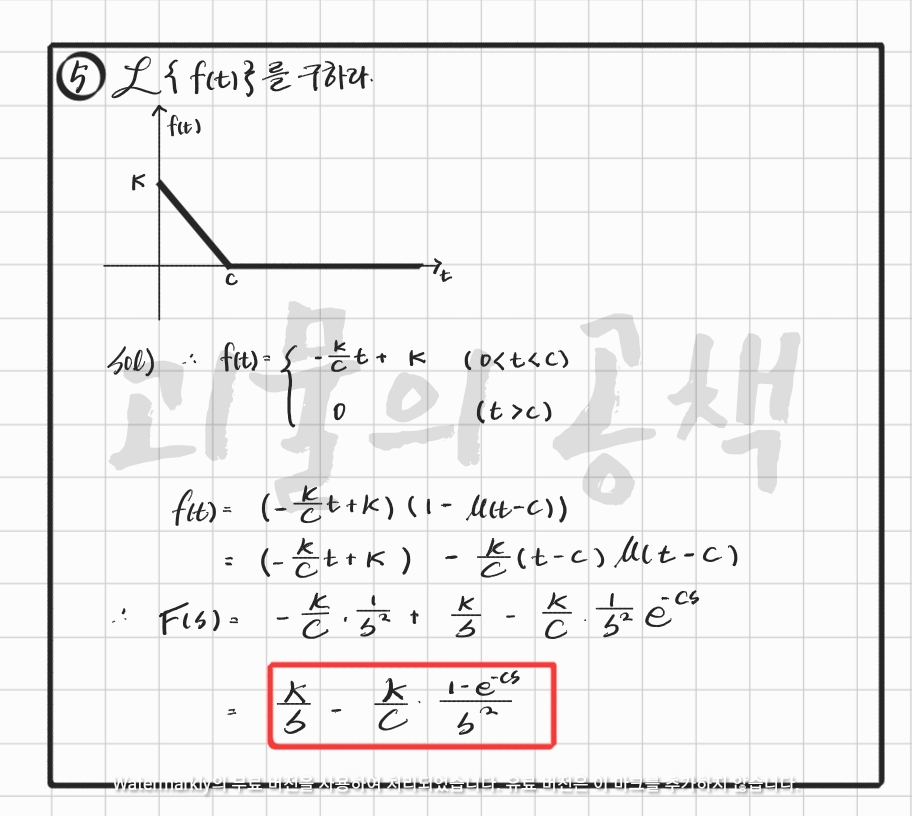
위처럼 단위계단 함수를 이용해주어도 되고,
혹은 라플라스 변환의 정의를 이용하여 직접 계산하는 방식도 좋다.
6.

ln이 들어가있으므로, 미분을 통해 익숙한 형태로 바꾸어준다.
라플라스 변환의 성질에 의해서, 역변환된 함수를 t로 나누어주면 답을 구할 수 있다.
7.

음.. 딱히 해줄 코멘트가 없다. 위 과정대로 천천히 풀면, 쉽게 풀어줄 수 있다.
8.

라플라스 변환의 합성곱 성질을 이용하면 쉽게 풀어줄 수 있다.
해설에서 사용한 스킬들은, 제가 작성한 괴물의 공업수학 1 전자책에 서술되어 있습니다.
자세한 설명은 아래 공지를 참조해 주시면 감사하겠습니다.
괴물의 공업수학 전자책을 판매중입니다.
안녕하세요! 여러분 제 전자책을 간단하게 소개하자면, 일종의 스킬 모음집이라고 할 수 있겠습니다. Part.1 은 Kreyszig 공업수학 기준, Part A(상미분방정식)과 Part B(선형대수) 에 해당하는 스킬들
atarax1a.tistory.com
'한양대학교 공업수학 > 공수1 기말 해설' 카테고리의 다른 글
| 한양대학교 공업 수학 1 - 01년도 기말 기출 풀이 (0) | 2024.05.17 |
|---|---|
| 한양대학교 공업 수학 1 - 00년도 기말 기출 풀이 (0) | 2024.05.16 |
| 한양대학교 공업 수학 1 - 99년도 기말 기출 풀이 (0) | 2024.05.15 |
| 한양대학교 공업 수학 1 - 97년도 기말 기출 풀이 (0) | 2024.05.13 |
| 한양대학교 공업 수학 1 - 96년도 기말 기출 풀이 (0) | 2024.05.11 |



