Problem
1. 다음 선형연립방정식의 해를 역행렬을 이용햐여 구하라.(5점)
$$
\begin{aligned}
-8 x+2 z & =1 \\
6 y+4 z & =3 \\
12 x+2 y & =2
\end{aligned}
$$
2. 다음 행렬의 고윳값과 고유벡터를 구하라. (5점)
$$
\left[\begin{array}{cccc}
0 & 0 & -5 & 7 \\
0 & 0 & 7 & -5 \\
0 & 0 & 19 & -1 \\
0 & 0 & -1 & 19
\end{array}\right]
$$
3. 다음 미분방정식을 풀어라. (6점)
$$
x y^{\prime}=y+\frac{2 x^4}{y} \cos \left(x^2\right)
$$
4. 다음 미분방정식을 풀어라. (6점)
$$
\left(e^{x+y}-y\right) d x+\left(x \cdot e^{x+y}+1\right) d y=0
$$
5. 다음 미분방정식을 풀어라. (6점)
$$
x y^{\prime \prime}+y^{\prime}=x \cdot\left(y^{\prime}\right)^2
$$
6. $x^2 y^{\prime \prime}+x(x-2) y^{\prime}-(x-2) y=x^3 e^x$ 의 해, $y_1=x$ 일때, 비제차미분방정 식의 일반해를 구하라.((6점))
7. 다음 미분방정식의 일반해를 구하라. (6점)
$$
y^{\prime \prime \prime}+25 y^{\prime}=32 \cdot \cos ^2 4 x
$$
Answer
1.
$$
x=0.25, y=-0.5, z=1.5
$$
2.
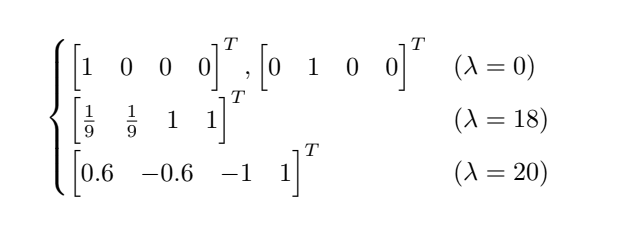
3.
$$
y^2=2 x^2 \sin \left(x^2\right)+c x^2
$$
4.
$$
x e^y+y e^{-x}=C
$$
5.
$$
y=-\ln \left|c_1-\ln \right| x| |+c_2
$$
6.
$$
y=x\left(c_1+c_2 e^{-x}+\frac{1}{2} e^x\right)
$$
7.
$$
y=c_1 \cos 5 x+c_2 \sin 5 x-\frac{2}{39} \sin 8 x+\frac{16}{25} x+c_3
$$
'한양대학교 공업수학 > 역대 기출문제' 카테고리의 다른 글
| 공수1 24년도 중간 기출 및 해답 (0) | 2025.04.16 |
|---|---|
| 공수1 23년도 중간 기출 및 해답 (1) | 2025.03.27 |
| 공수1 19년도 중간 기출 및 해답 (0) | 2025.03.27 |
| 공수1 18년도 중간 기출 및 해답 (0) | 2025.03.27 |
| 공수1 17년도 중간 기출 및 해답 (0) | 2025.03.27 |
