
양변을 xy로 나누어주는 것이 핵심이다.(사실 나누지 않아도 되는데, 그래야 꼴이 조금더 명확히 보인다.)
여기서 인수분해가 가능한데, 꼴이 보이지 않는다면, 근의 공식을 사용해주어도 괜찮다.
그려면, 각각의 해에 대해서 y를 구해줄 수 있다.
두 y모두 무한대로 갈때 0으로 수렴하는 것을 쉽게 알 수 있을 것이다.

siny를 치환하여, 베르누이 방정식을 풀어주는 형태이다.
그런데.. 과연 siny를 치환하려는 아이디어가 떠오를 수 있을까?
나라면 시험장에서 떠올리지 못했을 것 같다. 그래서 개인적으로 아래 풀이를 꼭 숙지하고 넘어가는 것을 추천한다.

적분인자 모듈 2형을 통해서, 적분인자를 어떻게든 짜내주는 것이 핵심이다.
이 방법을 사용하면, 모든 풀이 방법이 막혔을때도, 어떻게든 문제를 풀 수 있게 해준다.

이것도 신유형이다. 한해를 명시해주지 않고, 그냥 어떤 형태인지만 알려주는 형태이다.
그렇지만, 그리 어렵진 않다. 지수함수를 구해주고, 차수축소를 통해서 2번째 해를 구해주자.

이것도 신유형이다.
주어진 해에서 어떤 것이 제차해이고, 비제차인지를 구분해주는 과정이 추가적으로 들어가야 한다.
그래도, 이런 유형에 익숙하다면, 그렇게 어렵진 않을 것이다.

보조방정식의 해만 잘 구해주면 끝나는 문제이다.
비제차항의 경우는, 쉽게 24임을 알 수 있다.
(상수계수 전환 모듈을 사용한 후, 미정계수법을 적용해보자)
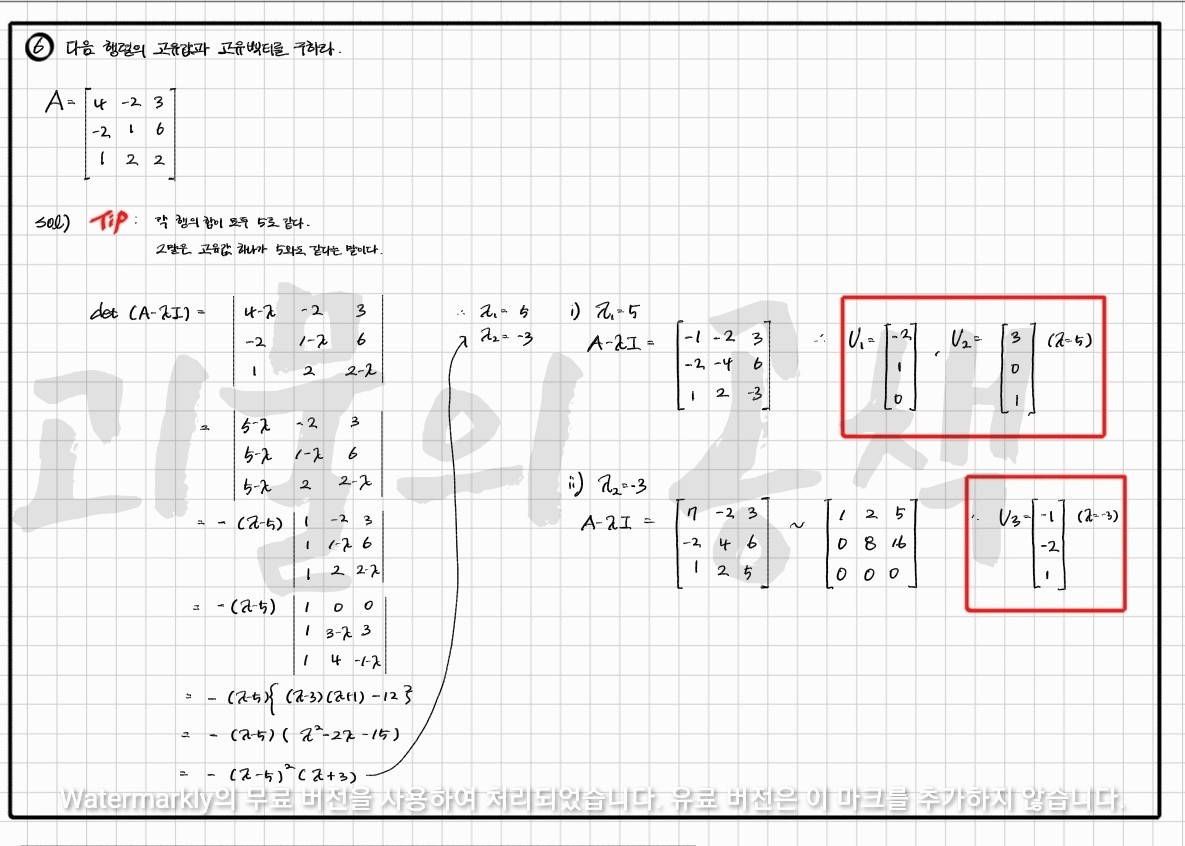
각 행의 모든 성분의 합이 5인 것을 이용한다.
그러면 행렬식을 계산하기 쉽게 만들어 줄 수 있다.
야무지게 계산해주자.
비제차항의 특이한 숫자에 집중하자
그러면 첫번째 행과 두번째 행의 합이 새번째 행이 되고,
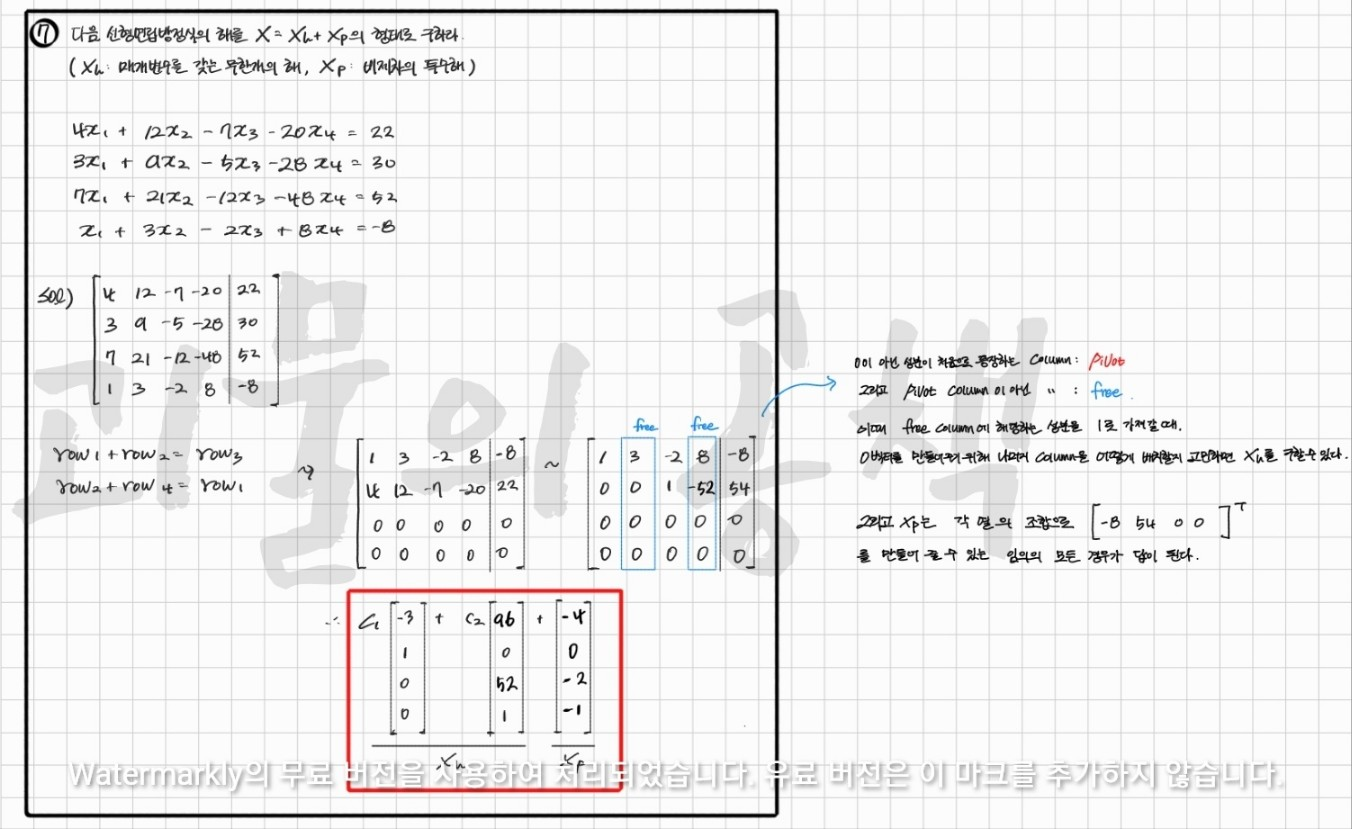
두번째 행과 4번째 행의 합이 첫번째 행이 되는 것을 알 수 있다.
그렇게 두 행을 날려버리면, 쉽게 해(벡터)를 구해줄 수 있다.
해설에서 사용한 스킬들은, 제가 작성한 괴물의 공업수학 1 전자책에 서술되어 있습니다.
자세한 설명은 아래 공지를 참조해 주시면 감사하겠습니다.
괴물의 공업수학 전자책을 판매중입니다.
안녕하세요! 여러분 제 전자책을 간단하게 소개하자면, 일종의 스킬 모음집이라고 할 수 있겠습니다. Part.1 은 Kreyszig 공업수학 기준, Part A(상미분방정식)과 Part B(선형대수) 에 해당하는 스킬들
atarax1a.tistory.com
'한양대학교 공업수학 > 공수1 중간 해설' 카테고리의 다른 글
| 한양대학교 공업 수학 1 - 선대 기출 모음(2) (1) | 2024.04.16 |
|---|---|
| 한양대학교 공업 수학 1 - 선대 기출 모음(1) (0) | 2024.04.16 |
| 한양대학교 공업 수학 1 - 21년도 중간 기출 풀이 (1) | 2024.04.13 |
| 한양대학교 공업 수학 1 - 19년도 중간 기출 풀이 (1) | 2024.04.12 |
| 한양대학교 공업 수학 1 - 18년도 중간 기출 풀이 (0) | 2024.04.11 |



